Easy row and column strategy in Killer Sudoku puzzles

In part two of a three part series on Killer Sudoku, we'll talk about row and column matching. Yesterday, we discussed basic strategies. We're finishing with an advanced counting strategy tomorrow.

A Killer Sudoku shared its basic rules with the regular Sudoku puzzle.

One of the rules of a Killer Sudoku puzzle is that a number must be unique on a horizontal row, in a vertical column and inside a block.

Let's look at how we can use this rule to solve a Killer Sudoku puzzle. 

Eliminate options

If you know that a number in a field is already definite, you can eliminate this number from all fields in that row, column or block. 

Have a look at this situation here. The 8 was given by the puzzle itself, the 7, 9 and pencilled numbers have already been deduced in this post on basic strategies. 

With an 8 in the bottom right corner, the 8 can no longer appear in any field on the bottom row.

So, the 8 is already on the bottom row in the right block.

That means in the left block, we can already eliminate the 8 on the bottom row. This will cross off both of the fields in the combinations with sum 9. 

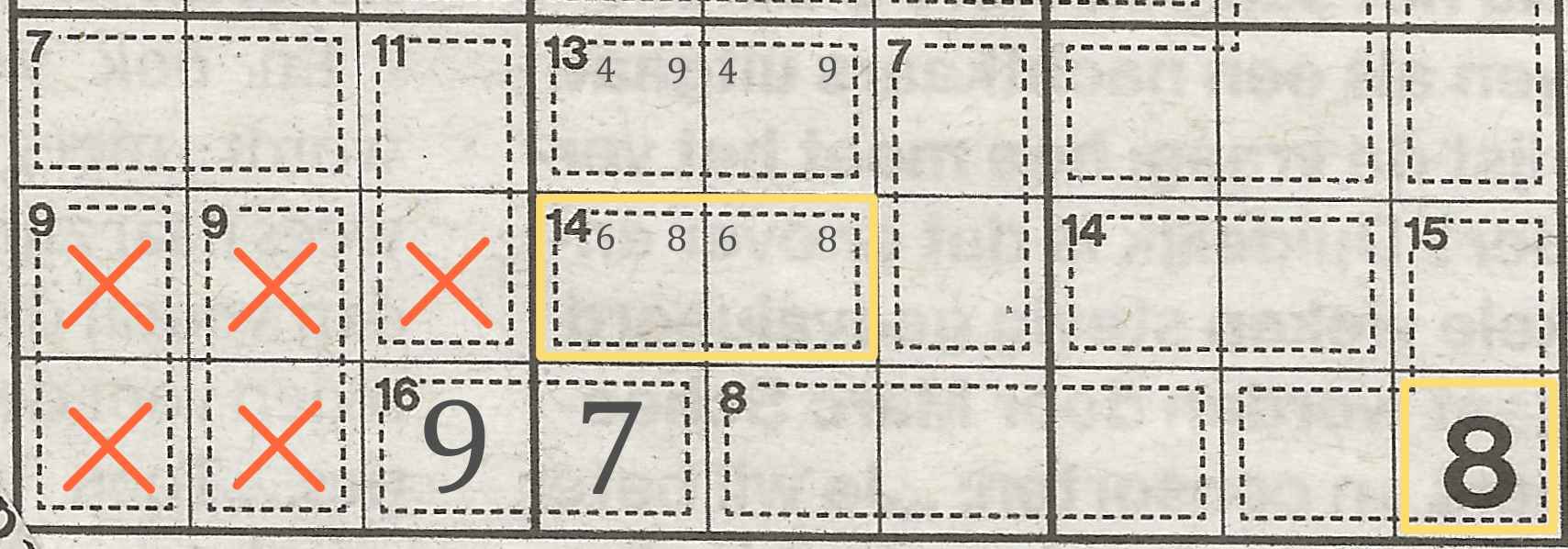
With the 8 used in combination 14 of the middle block, the 8 is no longer allowed in the middle line of the left block.

In the middle block, we have already deduced that the combination of sum 14 will be 6 + 8. 

Because of this, this will eliminate the 8 as an available number on the whole middle row. We have now ruled out 1 + 8 as an eligible combination for both combinations with sum 9. 

The 8 is only allowed of the top row in the left block. As 8 isn't used in a combination with sum 7, it must go in the combination with sum 11.

That leaves the top row of the left block. 

The top row is made up of 2 combinations: a full combination of sum 7 and one field of a combination of sum 11. 

Obviously the 8 won't fit in the combination of 7, which automatically means that the 8 will have to go in the top field in the combination of 11. 

Don't use pencilled numbers with different orientation

Now, while solving the middle row of the left block, we know knew there couldn't be an 8. Why? Because

• in the middle block, the 8 is already used in the combination of 14; AND
• a number can only appear once on every row.

This is the basic Sudoku rule. 

Be careful though: you can't use a vertical combination to exclude a number on a horizontal row!

Let's take a look at this example. It's the same puzzle as before. We filled in the 8 and added the 3 to make up a sum of 11. We also deduced the combination of 7 in the middle block to be 2 + 5. 

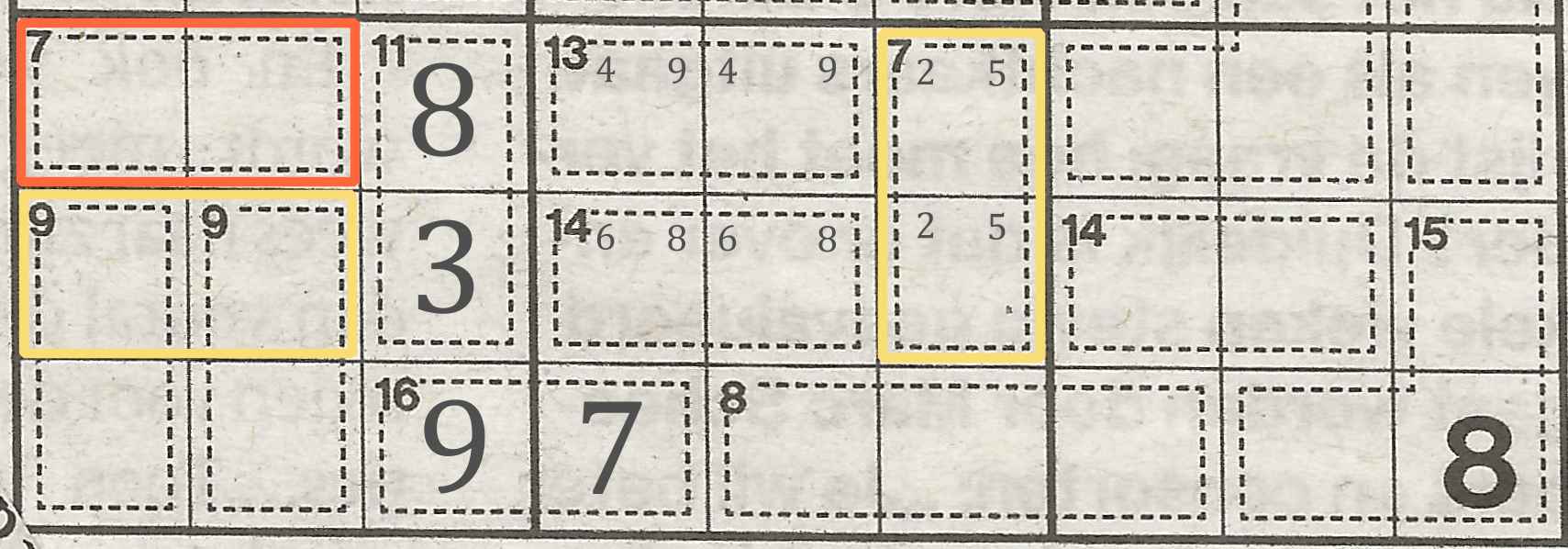
You can't take a vertical combination and use it to deduce a horizontal row... or can you?

In the left block you might be tempted to use this 2 + 5 combination to rule out numbers 2 and 5 for both the combinations of 9. DON'T!

Even though you know that the bottom field of that combination of 7 is a 2 or 5, it's exactly that: 2 OR 5.

If it's a 2, the 5 can be used in the left block. Similarly, if it's a 5, the 2 can be used in the left block. Even 'worse': the 2 and 5 can still go in the bottom row, leaving both 2 + 7 and 5 + 4 combinations valid for the left block.

Exception: use pencilled numbers with different orientation

There is an exception to the rule which does let you use pencilled numbers in a different orientation. Let's have a look at the top row.

We know a combination of 7 can be made up of 1 + 6, 2 + 5 or 3 + 4. 

3 + 4 is a no go, as:

• the 3 is already used in the combination of 11; AND
• a number must be unique within a block.

Can we use 2 + 5? We just said that you can't exclude a combination on a row based on a vertical combination in another block, right? 

In this case, even that vertical combination affects this horizontal combination for 7. Why?

• If the combination in the middle block has the 2 on top and 5 below, it excludes 2 from that row. In the left block, we can no longer use 2 + 5.
• If the combination in the middle block has the 5 on top and 2 below, it excludes 5 from that row. In the left block, we can no longer use 2 + 5.

Regardless of the order in which the 2 + 5 combination is used, either 2 or 5 are ruled out. As the 2 and 5 are both essential to make up a combination of 2 + 5 (duh), this excludes the 2 + 5 combination for sum 7 in the top row of the left block.

This leaves 1 + 6 as the only possible combination.

Continuing on

Now, of course this means that for the both combinations of 9 we should use the 2 + 7 and 4 + 5. In this case, we don't know which combination is used for which sum. 

What we can say, is that the 7 is already used in the bottom row. That means for the combination of 2 + 7, the order will be 7 on top and 2 below. 

Also, see that 14 in the right block? In the basic strategy post we already pencilled in the combination 5 + 9. That means we know the 5 can't go on that row any more, making the combination of 7 in the middle block 5 on top and 2 below.

This places a number 5:

• On the top row, in the middle block; AND
• On the middle row, in the right block.

The only row left for a 5 is the bottom row, which means the combination of 4 + 5 will have 4 on top and 5 below.

With all but one field pencilled in, we are ready to fill in the final number on that middle row.

To conclude this post, we have defined or pencilled in the middle row completely, apart from the field on the far right. 

If we check all the numbers, only the number 1 is missing in this row. This makes it easy: the 1 can be filled in on the far right field. It will sit together with the 8 in the combination of 3 for sum 15. 

And of course, that means the third field of this combination for sum 15 will be...?