Try these 3 basic Killer Sudoku strategies every time

In part one of a three part series on Killer Sudoku, we'll talk about basic solving strategies. Part two will dive deeper in line matching tomorrow, finishing with an advanced counting strategy on Monday.

Puzzles can be great fun. Even if their name is Killer Sudoku, which, admittedly, does sound a little scary. 

But even Killer Sudoku puzzles can be solved. And trust me, you don't need to be a Nobel prize winner to do so. 

With these 3 basic strategy, you will come a long way in solving your Killer Sudoku!

Killer Sudoku rules

To know how to solve a Killer Sudoku puzzle, we first need to know the rules. 

A Killer Sudoku, like it's big brother the Sudoku, consists of a grid of 3x3 blocks, so 9 blocks in total.

Each block is made up of 3x3 fields. So 9 fields per block, 81 fields in total. 

Every field is part of a combination. A combination always spans multiple fields and can combine fields from different blocks. 

To solve the puzzle, each field will hold a number. This number must adhere to the following 5 rules:

1. Each number must be unique (so can only occur once) in a block;
2. Each number must be unique in a line (horizontal);
3. Each number must be unique in a column (vertical);
4. Each number must be unique in a combination.
5. The numbers inside a combination must add up to the sum depicted in the combination. 

A combination is often indicated by a dashed line spanning multiple fields. In the upper left corner of a combination, a sum is printed over the dashed line. 

With these 5 rules in mind, here are 3 simple steps to get you on your way to solve your Killer Sudoku.

A note on terminology

Talking about blocks, lines, fields... it can become confusing pretty quickly. 

To let you know which block we're looking at, we'll work with shorthand notation:

• TR: Top Row;
• MR: Middle Row;
• BR: Bottom Row;
• LC: Left Column;
• MC: Middle Column;
• RC: Right Column.

Some examples:

• TRMC is Top Row, Middle Column;
• MRMC is Middle Row, Middle Column - the block at the center;
• BRRC is Bottom Row, Right Column - the block in the bottom right corner.

So, without further ado: let's start on the 3 most basic theories for you to solve Killer Sudoku puzzles!

Strategy 1: Fill in all 3 and 4 combinations

It has already been mentioned that each number must be unique in a combination.

The key to combinations is: If you add up all the numbers in the combination, the total must match the sum of the combination. 

Knowing that we can only use every number once in a combination, we already know the numbers which belong to the sums of 3 and 4. 

A combination with sum of 3 will always consist of the numbers 1 and 2. 

A combination with sum of 4 will always consist of the numbers 1 and 3. That is because 2 and 2 isn't allowed, numbers in a combination must be unique. 

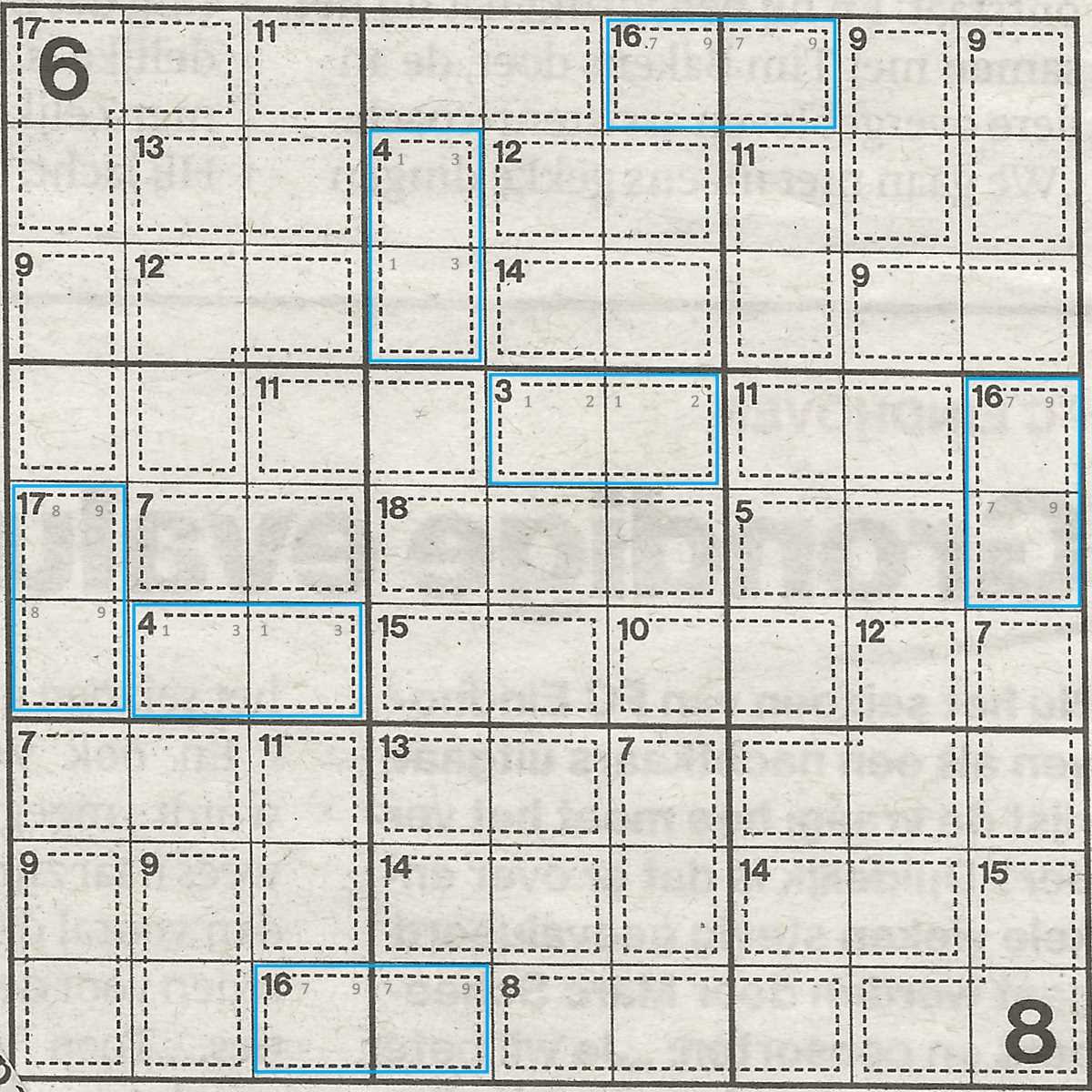
Start a game of Killer Sudoku by checking for sums of 3, 4, 16 and 17.

So when starting a Killer Sudoku, grab your pencil and just go through all the lines one by one. Search for combinations with sum 3 and 4. Write these combination really lightly inside the fields. We don't necessarily know which field will be 1 and which will be the 2 or 3 , but we know that they will both hold either number.

Note: A sum of 5 will either consist of 1 and 4 OR 2 and 3. So that combination isn't a clear shot. Don't fill those in yet. 

Strategy 2: Fill in all 16 and 17 combinations

In the same way of 3 and 4, we also already know the numbers which belong to the sums of 16 and 17. 

A combination with sum of 17 will always consist of the numbers 9 and 8. 

A combination with sum of 16 will always consist of the numbers 9 and 7. That is because 8 and 8 isn't allowed, numbers in a combination must be unique. 

Scroll your eyes across every line to see if you have a combination for 16 or 17. Write these combination really lightly inside the fields. As before, we don't necessarily know which field will be 9 and which will be the 7 or 8 , but we know that they will both hold either number.

Note: A sum of 15 will either consist of 6 and 9 OR 7 and 8. So that combination isn't a clear shot either.

Strategy 3: Check for horizontal, vertical or block combinations

Once you pencilled in all those possibilities, you can check for the blocks, horizontal lines and vertical colums.

For instance, in this example image, the number 8 is given in BRLC (bottom row, right column). In the block, there is also a combination of sum 14.

A combination of sum 14 can either be 6 + 8 or 5 + 9. But, you know that:

• you already used 8 (it was given); AND
• numbers in columns must be unique.

You now know the combination for 14 will have to be 5 + 9.

This happens inside the same block, but the same is true for lines and columns. 

On the same line but one block to the left (BRMC), there is another combination of 14.

And again, a combination of 14 can either be 6 + 8 or 5 + 9. But, you know that:

• you already used 5 + 9 (we don't know in which order, but we know that they will be on that same line); AND
• numbers in lines must be unique.

You now know that the combination for 14 in this block will have to be 6 + 8.

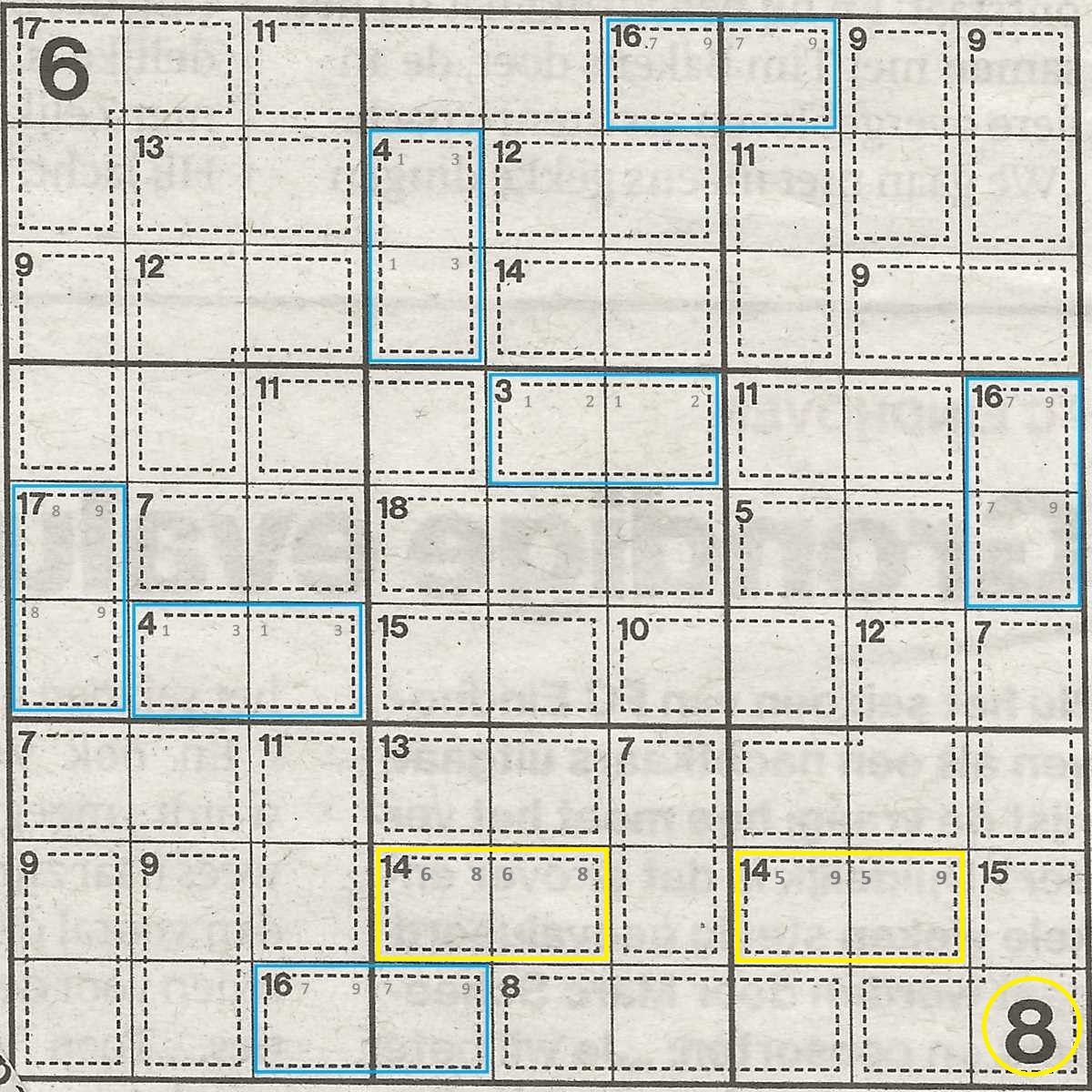
Check your blocks, lines and columns for possible combinations and get rid of those that are not eligible.

Following on that logic and going back to the scope of the BRMC (bottom row, middle block): 

A combination of 13 can either be 4 + 9, 5 + 8 or 6 + 7. But we can see that:

• 5 + 8 can't be used, as the combination of 14 already uses the 8; AND
• 6 + 7 can't be used, as the combination of 14 already uses the 7; AND
• numbers in blocks must be unique.

We now know the combination with sum 13 can only be 4 + 9. 

In step 2, we pencilled in 7 + 9 for the combination of sum 16 spanning across the left 2 blocks on the bottom row.

With the 9 used in the combination with sum 14 in the middle block, we now that a 9 can never happen in that same block. That means the 9 must be in the left field of the combination (different block), leaving the 7 for the right field of that combination with sum 16 (middle block). 

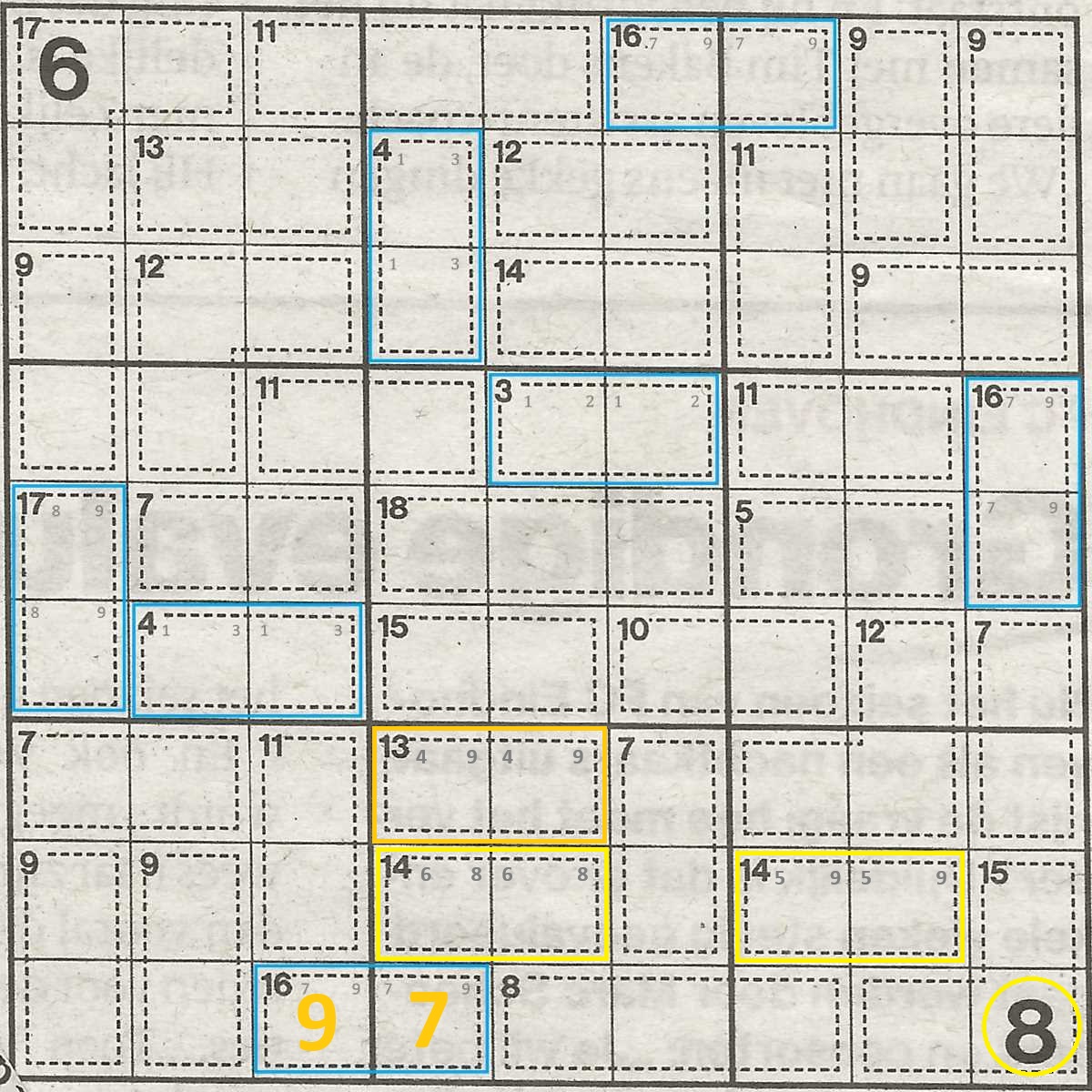
If a combination spans 2 blocks, sometimes this means you can easily know which number belongs to which field. In this case, of the 7 and 9, only 7 is eligible as a number in the right field / middle block. It can't be 9, because in that middle block, the 9 is already used for the 13 combination.

We can keep taking this further, one step at a time.

1. Combination with sum 7 in the BRMC, must be 2 + 5, as both 1 + 6 and 3 + 4 are ruled out. The 4 and 6 are already used for other combinations.
2. That means Combination with sum 3 in MRMC, must be written as 2 | 1. The right field of this combination is in the same column as the 2 + 5 of step 1. And even though we don't know in which exact field the 2 or 5 will be, we know there will be a 2 in that column. 
3. For BRMC, we are now only missing the numbers 1 and 3. That must be written as 1 | 3, as the 1 is placed in the third column of MRMC (see step 2).
4. That leaves the combination of 8 spanning BRMC/BRRC. In step three, we placed 1 + 3 in BRMC. 8 - 3 - 1 = 4. The 4 goes in BRRC. 

Bonus strategy: Don't jump to conclusions

The last step might lead you to jump to a conclusion you're not ready to take. 

There is a combination of sum 7 spanning MRRC/BRRC. Let's recap what we know so far:

• We know a combination of 7 can be made with 1 + 6, 2 + 5 or 3 + 4. 
• We also know that 5 is already used in the BRRC by the combination of 14.
• We also know that the 4 is already used in the BRRC by the combination of sum 8 we filled in in step 4. 

That could make you think "that leaves 1 + 6 for the combination of 7."

While this might end up to be true, it doesn't need to be like that. Here's why:

• To use the combination of 2 + 5, the 5 would just have to be in the middle row, leaving the 2 for the bottom row. Perfectly valid.
• The same is true for the 3 + 4. While it is true that you can't use the 4 in the bottom row, it is perfectly valid in the middle row. 

The most important thing with these Killer Sudoku puzzles is to take your time. Don't be too hasty and don't jump to conclusions.