Can you count to 45? Solve a Killer Sudoku quickly with this simple strategy!

This is the last part of a three part series on Killer Sudoku. We started day 1 with basic strategies. Yesterday, we had a deeper dive on row strategies. Today, you will learn a more advanced method for solving combinations spanning multiple blocks.

Killer Sudoku puzzles are a variant on the traditional Sudoku puzzle. 

Like a Sudoku, you are playing a 9x9 grid, divided in 3x3 blocks. Numbers ranging from 1 to 9 are used, but they must be unique in blocks, columns and rows. 

Killer Sudoku adds the extra challenge of combinations. Either inside a block or even spanning across multiple blocks, combinations give you a sum to which the numbers inside the combination must add up to. 

Just getting started with Killer Sudoku puzzles? Have a look at our basic guide first!

Count to 45

So every block, every horizontal line and every vertical line has all the numbers from 1 to 9. 

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45. 

That means for every block, horizontal line and vertical line, all the numbers total 45.

We can use this knowledge to our advantage.

Combinations spanning blocks - 1 field outside

The combinations which make a Killer Sudoku so... killing 😉 can be a blessing, but also a curse. Especially when a combination spans across multiple blocks, it can be tricky to fill correctly. 

But sometimes, these combinations across blocks are actually quite handy. That is because we already learned that all the numbers in a single block added together, must add up to 45 in total. 

That means that we can deduce the following theory:

Given there is a block, of which 1 combination has 1 (or more) fields in a different block, we can sum up all the combinations and detract 45. The remainder is the number for the field outside of the block.

Here's a Killer Sudoku puzzle we will use as an example. 

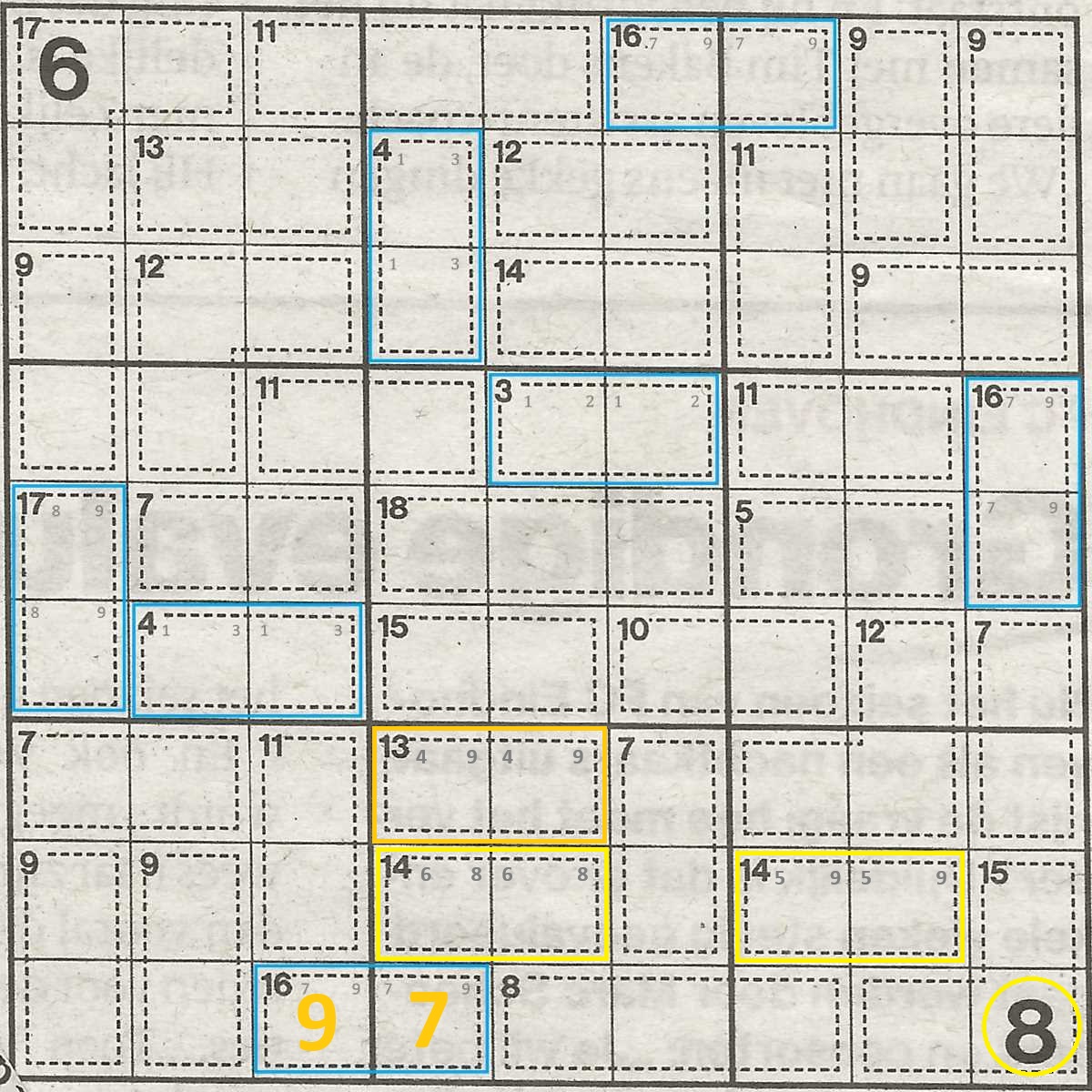
If a combination spans 2 blocks, sometimes this means you can easily know which number belongs to which field.

Have a look at the block in the Top Row, Right Column. In this block, there are:

• 3 times a combinations of sum 9;
• A combination of sum 11;
• half of a combination of sum 16.

For a sum 16, we already know that the combination must be 7 + 9. But even if we didn't, we would have been able to calculate it. 

Let's go back to the theory for a moment.

• Given there is a block of which 1 combination has 1 (or more) fields in a different block
  • Look, the combination 16 has 1 field outside of the block
• we can sum up all the combinations 
  • 9 + 9 + 9 + 11 + 16 = 54
• and detract 45
  • 54 - 45 = 9
• The remainder is the number for the field outside of the block
  • That means the field of this combination in the Top Row, Middle Column is 9
  • That also means the field in the Top Row, Right Column is 7

How does this help us?

Well, we now know 2 + 7 is no longer a viable combination for 9. That leaves 1 + 8, 3 + 6 and 4 + 5. As we have 3 combinations of 9 to fill, all of these combinations will be used. Which means the combination for 11 will have to be 2 + 9. 

And just like that, you pencilled in all combination in a block!

Combinations spanning blocks - 1 field inside

There is another way you can use the magic number 45 to your advantage. In the case of the example above, it doesn't really matter which way you choose. In other cases, where more of the fields are outside of the block and only 1 inside, you need to calculate differently. 

Instead of adding up all combinations and subtracting 45, you are adding up only the combinations inside the block.

Given there is a block, of which 1 combination has 2 or more fields in a different block and only 1 in the block itself, we can sum up all the combinations completely inside the block. If we subtract the sum from 45, the remainder is the number for the field inside the block. 

Using the same example as above, we take the same combinations:

• 3 times a combinations of sum 9;
• A combination of sum 11;
• half of a combination of sum 16.

If we now follow this new strategy:

• Given there is a block, of which 1 combination has 2 or more fields in a different block and only 1 in the block itself,
  • There are 3 combinations of sum 9 and 1 combination of sum 11 fully inside the block
  • Of the combination with sum 16, only 1 field is inside the block
• we can sum up all the combinations completely inside the block.
  • 9 + 9 + 9 + 11 = 38
• If we subtract the sum from 45,
  • 45 - 38 = 7
• the remainder is the number for the field inside the block. 
  • That means the field in the Top Row, Right Column is 7
  • That also means the field of this combination in the Top Row, Middle Column is 9

Of course, we already knew this by going the other way around. But at least, now we proved our point.

Multiple combinations spanning blocks

So far, we have worked on the premise that you can only use this theory with single combinations going outside a block. If a block has multiple combinations crossing into other blocks, it is usually not possible to use this theory. 

But, if you filled in the field in one of those combinations, it still might be. 

Even when multiple combinations span across different blocks, you can still use this 'count to 45'-theory.

Using the same puzzle as above, have a look at the left and middle block on the top row and grab the theory. 

• Given there is a block of which 1 combination has 1 (or more) fields in a different block
  • No, this one has 2 combinations; but...
  • One of those combinations is already filled in AND we know that the 9 is in the field of this block
• we can sum up all the combinations 
  • 4 + 12 + 14 + 9 (only count the 9 inside the block, not 16 for the combination) + 11 = 50
• and detract 45
  • 50 - 45 = 5
• The remainder is the number for the field outside of the block
  • That means the field in the Top Row, Left Column is 5
  • That also means the 2 fields of the combination in the Top Row, Middle Column have to sum up to 6. 

How does this help us? 

Well, we already know that the combination of sum 4 in the middle block takes up 1 + 3. That means that combination 1 + 5 is unavailable for our new sum 6, leaving only 2 + 4 as a possible combination. 

With 1, 2, 3 and 4 taken, the combination for sum 12 must be 5 + 7, leaving 6 + 8 for 14.

And again, a whole block pencilled in with the correct combinations!

Combinations in a row

This strategy doesn't only work for blocks. It also does wonders for solving rows or columns!

Have a look at the middle row of blocks for a moment:

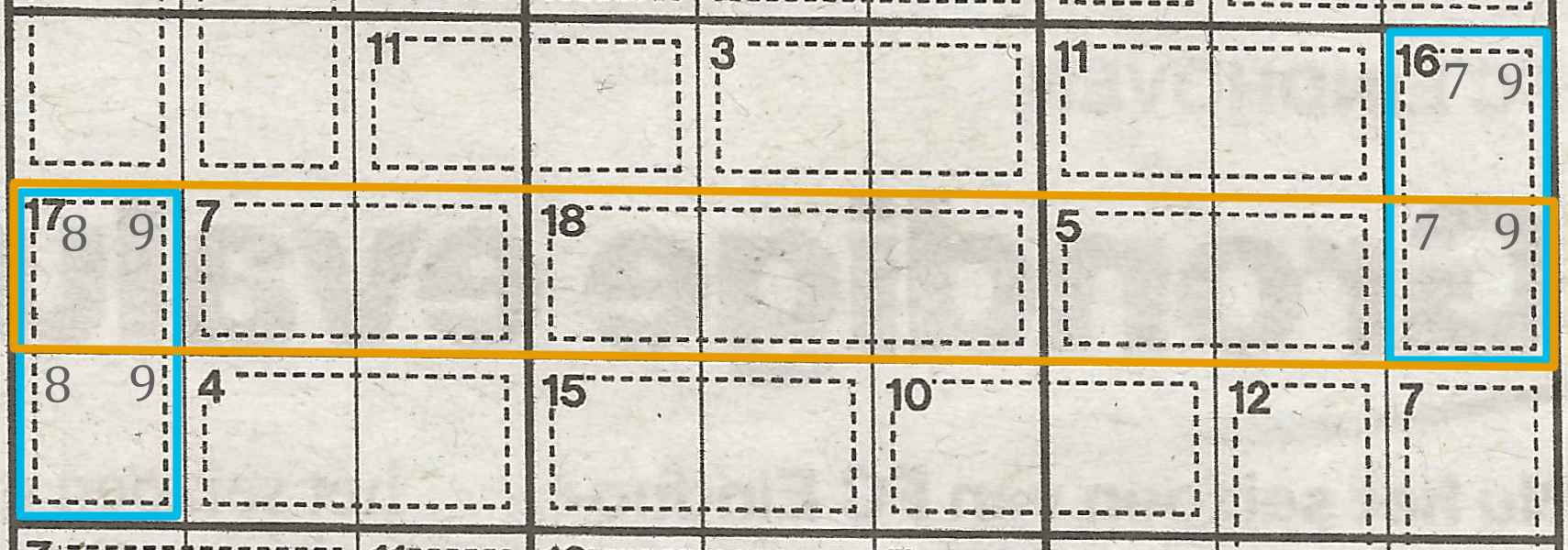
The magic number 45 also works when counting combinations for a row or column.

From left to right, the highlighted row in orange consists of:

• Half of a combination of sum 17;
• A combination of sum 7;
• A combination of sum 18;
• A combination of sum 5;
• Half of a combination of sum 16.

You might be thinking: "there are 2 combinations with a field outside of the row, I cannot use this information." If you are, it is understandable but you are wrong! 

We already know:

• The combination for sum 17 is always 8 + 9;
• The combination for sum 16 is always 7 + 9;
• 7 + 18 + 5 = 30;
• 45 - 30 = 15.

The combinations for sums 7, 18 and 5 are all completely on the same row. We can add them together, which makes 30 in total.

As all numbers in a row must add up to 45, that leaves the 2 outer fields to make up for the rest. Detract the sum of the other combinations (30) from 45, we have 15 remaining.

That means for the fields in the highlighted row in orange, the fields part of the combinations of sum 16 and 17 must make up 15 in total. 

The only way this is possible, is by using:

• the 7 from the combination with sum 16 at the right;
• the 8 from the combination with sum 17 on the left;

While we had 2 combinations with fields outside of the row, using this magic number 45 method we were still able to deduce the number in 4 fields!

A perfect theory

Having several useful theories in your puzzling tool belt is great when trying to solve Killer Sudoku puzzles. 

45 is a magic number. Given there is a block, row or column, of which 1 combination has 1 (or more) fields in a different block, we can

• sum up all the combinations and detract 45. The remainder is the number for the field outside of the block, row or column; OR
• sum up only the combinations fully inside the block, row or column. The difference between the sum and 45 is the number for the field inside of the block, row or column.

Remember this strategy! It does seem a little advanced, but it's actually pretty useful. 

And of course, have a look at the 3 beginner strategies to solve Killer Sudoku puzzles if you are just starting out!